Determining if a point is in a polygon (or the point in polygon problem) is a case of point location problems. It has particular applications in processing geometric data, such as computer graphics, geographic information systems, and computer aided design (CAD), to name a few.
There are two main techniques used to solve this problem: ray casting and angle summation. This post will detail how the former can be applied practically to solve the problem.
Ray Casting
This technique is based on the observation that when travelling from infinity to a point within a polygon, you must go from the outside to the inside. This could happen many times but to eventually end up inside the polygon you must cross a boundary an odd number of times.
Point to be checked (P) = (3, 2).
Points that form the fence (in order) (ABCD) = [(-2, 3), (4, 4), (3, -2), (-1, -1)].
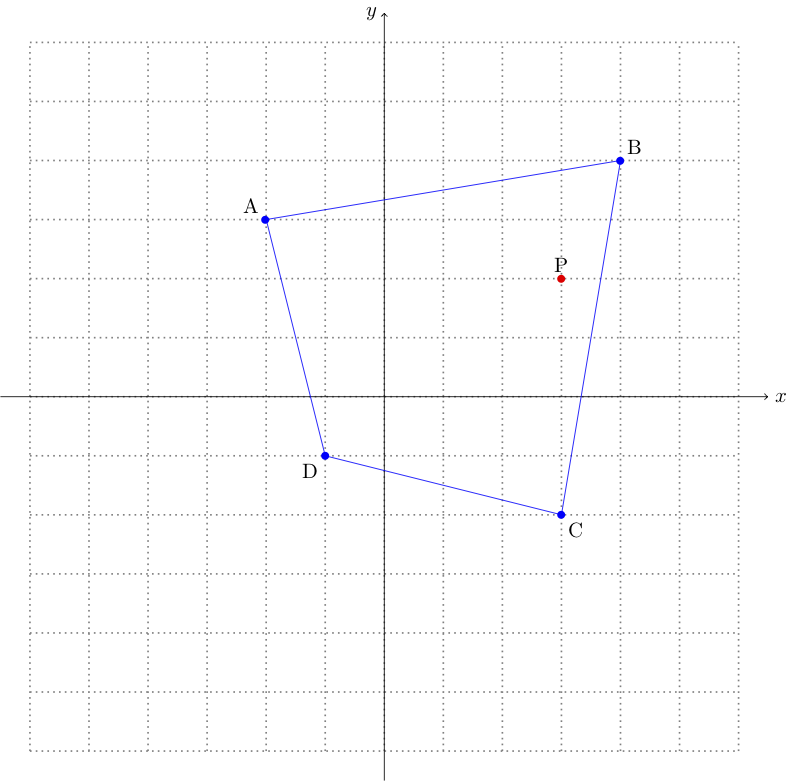
Figure 1
As you can see in Figure 1, the fence is shown in blue and the point to be checked in shown in red. The point is clearly inside the fence, but calculating a proof of this is not quite that easy.
Knowing that a ray cast in any direction from the point will intersect with the polygon an odd number of times if it is within the polygon, we can first form a line equation through the point to be checked that will be used as the ray. I’ve chosen to use a horizontal line, but a line of any gradient will work so long as it passes through the point.
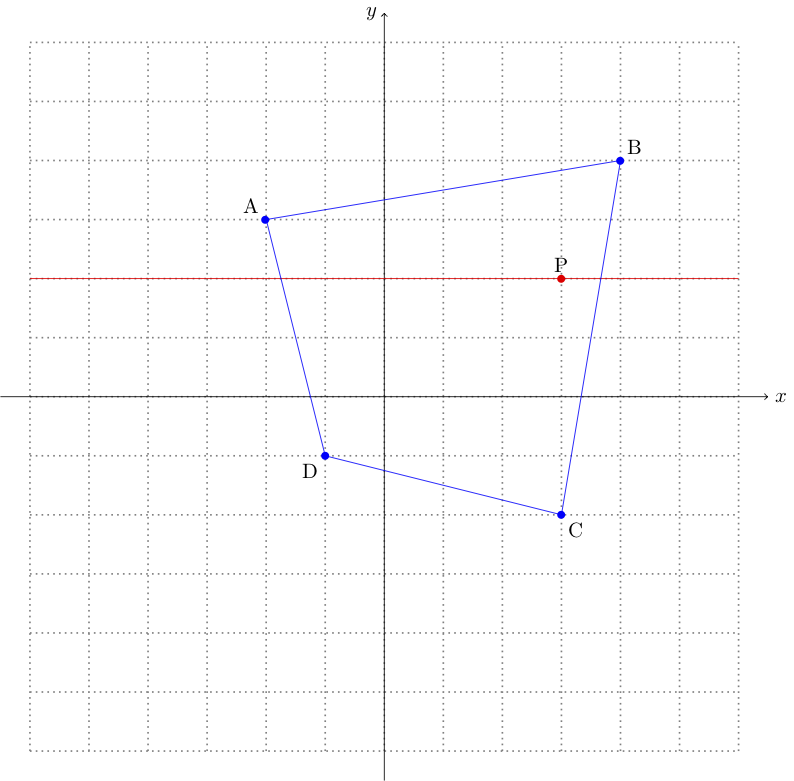
Figure 2
As you can see in Figure 2, the line drawn through the point (the point horizon line) intersects with the polygon once in each direction from the point. Hence, a ray cast from the point in a positive x direction will intersect with the fence once, and a ray cast in a negative x direction will intersect with the fence once. This asserts that the point is within the polygon because a ray cast in either direction intersects with the polygon an odd number of times.
However, a computer cannot just see that the lines intersect, this must be calculated. This is done using some simple coordinate geometry.
First, the equations of the lines that form the polygon are calculated. The polygon is separated into pairs of points: (A, B), (B, C), (C, D), (D, A), each pair forms a line that makes up part of the polygon. For each pair of points, the gradient is found. Taking (A, B) as an example:
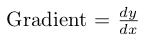
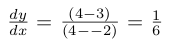
Figures 3 & 4
Once the gradient of the line has been calculated, the equation of the line can be found as follows:
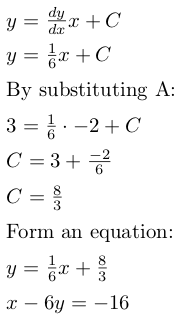
Figure 5
This is repeated for each pair of points.
Once the line equations of each side of the polygon have been found, we can find the intersects between them and the point horizon line. All pairs of line equations will have an intersect unless they are parallel, and so just counting the number of intersects cannot be relied upon to prove that the point is/is not within the fence polygon. This issue can be solved by performing a check to ensure that the point of intersection is within the area bound by the points that form the fence segment of the line that is being checked. Bearing this in mind, we can proceed to calculate the intersects between the point horizon line and the polygon.
The point at which 2 linear equations (straight lines) intersect can be calculated by solving these equations simultaneously, using Cramer’s rule. From Figure 2 we can see that the point horizon line intersects with lines BC and DA, for this example we will be using line BC, follow the above steps to find the equation for it.
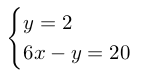
Figure 6
In very simplified terms, Cramer’s rule calculates the solutions to a system by finding the determinant of the matrix formed by the x&y coefficients (D), the determinant of the matrix formed by the y coefficient and the right-hand-side (Dx), and the determinant of the matrix formed by the x coefficient and the right-hand-side (Dy). Once these have been found, the solutions x and y can be found by calculated by Dx/D and Dy/D:
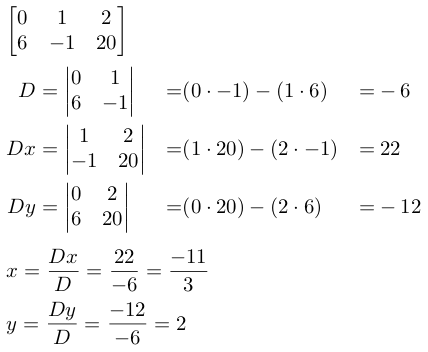
Figure 7
A much more detailed step by step explanation of Cramer’s rule can be found on Wolfram Mathworld.
If the determinant D is equal to 0, then the equations do not intersect (with linear equations this essentially means that the lines are parallel). If the determinant is not 0, we can proceed to calculate the point of intersection.
Once all points of intersection have been calculated, we will have 2 lists: a list of points less x-positive than (to the left of) the point being checked, and a list of points more x-positive than (to the right of) the point being checked. If the length of both of these lists is an odd number, then the point can be asserted to be within the polygon.
To try and phrase this differently, imagine walking the horizontal line from x = -∞ to x = +∞ through the point being tested. If, when walking, you cross an odd number of lines before you meet the point, and an odd number of lines between the point and +∞, then you can be pretty sure that the point is within the polygonal fence (excluding a few rare edge cases).
Conclusion
Ray Casting can be used to determine if a point is within a polygon (or geofence). This technique is applicable to geographic calculations, BUT… when working with latitude and longitude, it’s important to be careful calculating the distance between points. Checking if a point lines within a fence of other points however, is comparably trivial!
If you’re looking for a way to do this programmatically, I’ve written a (still W.I.P) a library in Python, called picket that performs this maths for you. Please contribute if you can!
Sam